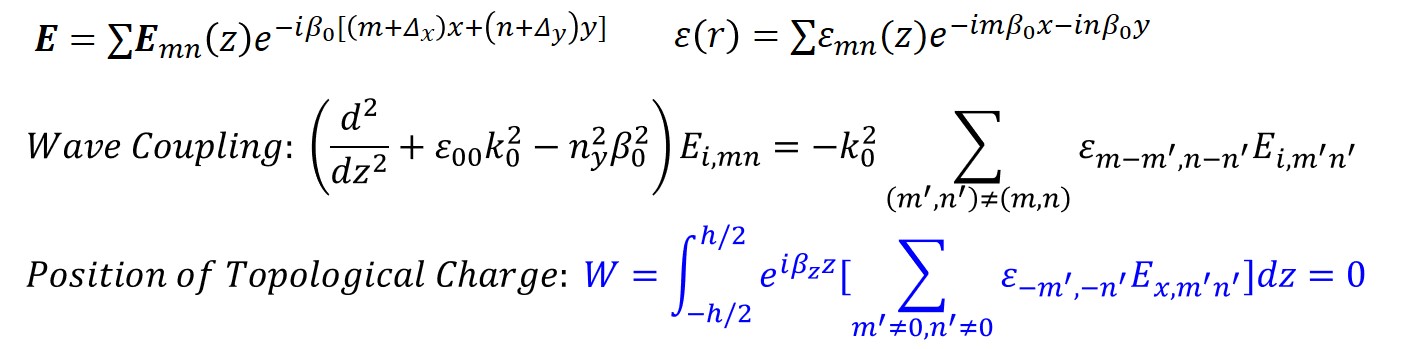Undergraduate Research on Topological Photonics
The first exploration of polarization vortices outside the first Brillouin zone. A collection of work that includes both theory and simulation of Bound States in the Continuum(BICs) and polarization vortices.
In Short
Existing works only focus on bound states in the continunm(BICs) and polarization vortices near the Γ point. This is the first work that studies a polarization vortex within the light cone but outside the first Brillouin zone. Both simulation and mathematical analysis of this phenomenon are performed. Utilizing the method developed and the polarization vortex found in this project, follow-up work(nature communications) realized a single-mode laser with distinct topological characteristics. The work was carried out at the School of Physics, Peking University.
Introduction: Photonic Crystal Nanolaser, BICs and Topological Protection
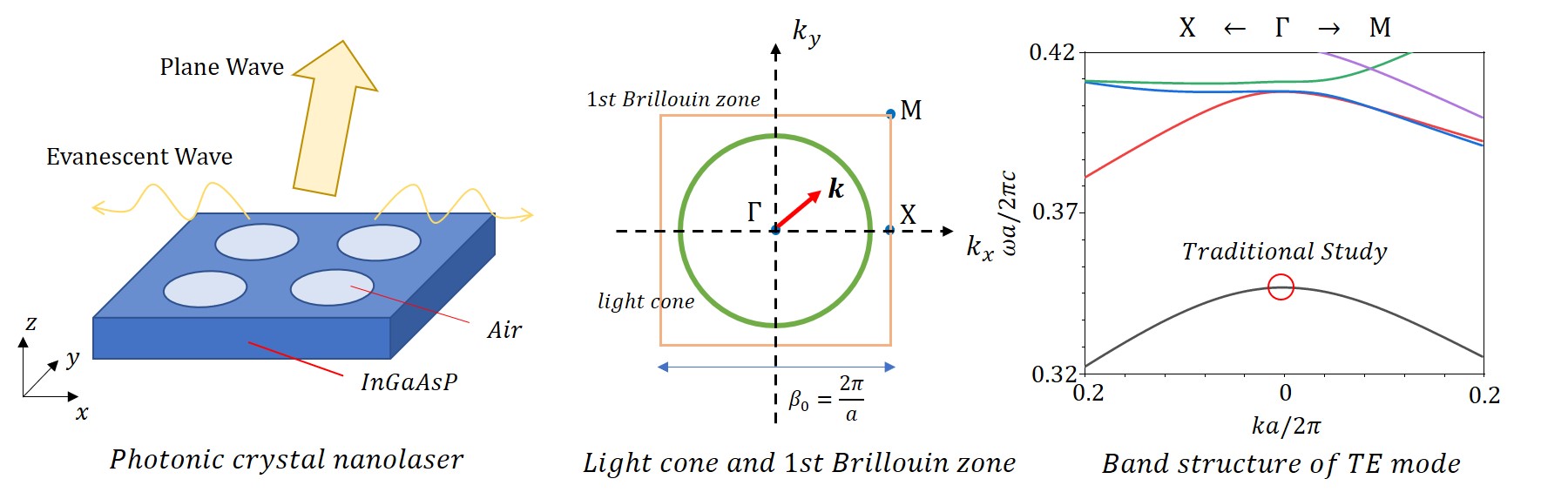
Photonic crystals are optical materials with wavelength-scale periodic structures (the name comes from ordinary crystals). Leveraging their ability to confine light, together with gain material like InGaAsP, these structures can be used as laser cavities.
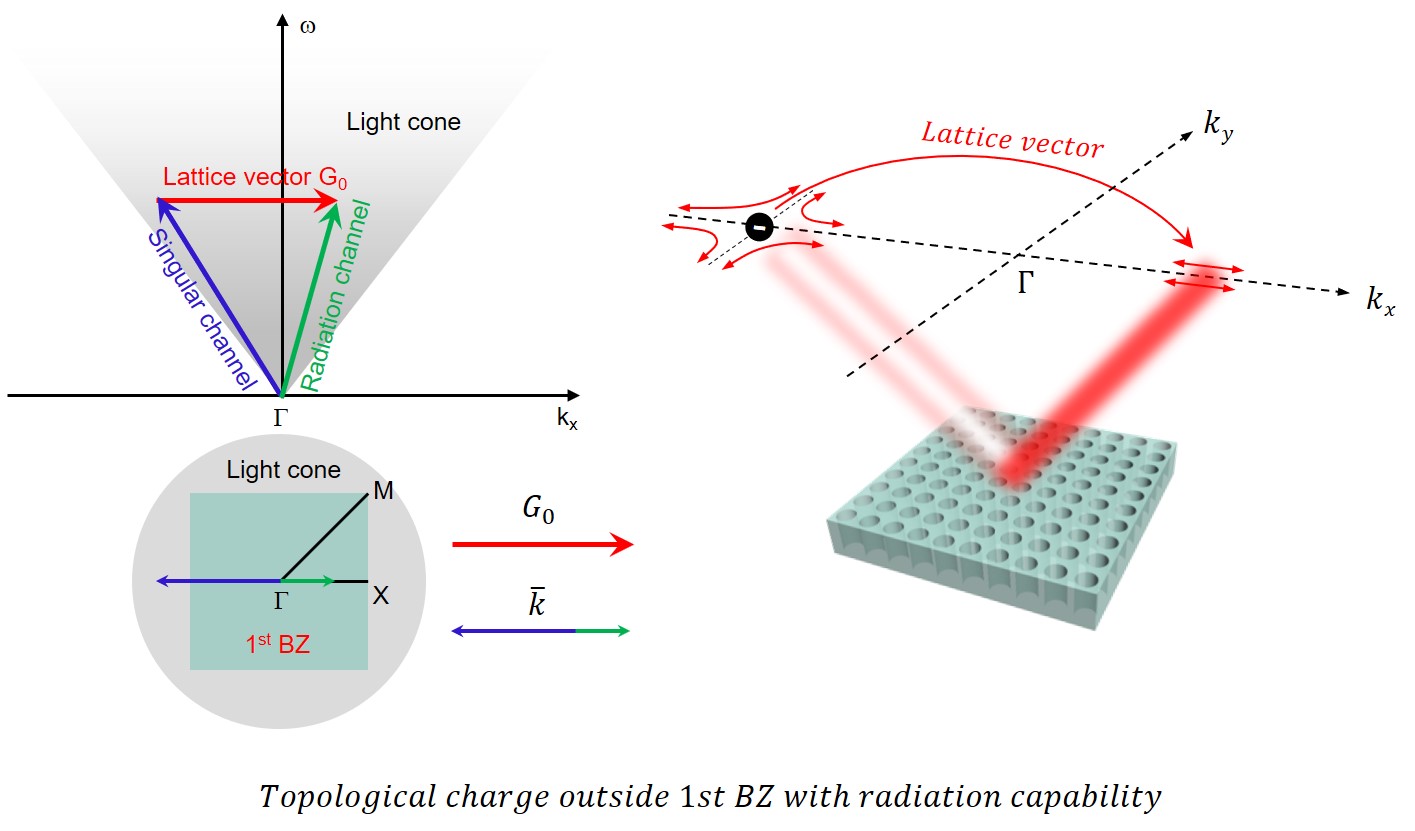
In the typical design, the light cone is smaller than the first Brillouin zone, which means each eigenmode with a reduced wave vector inside the 1st Brillouin zone can excite at most one plane wave in the free space
One approach to realize the lasing effect is to leverage special eigenmodes called BICs, for example, the indicated mode at Γ point in the first TE band.
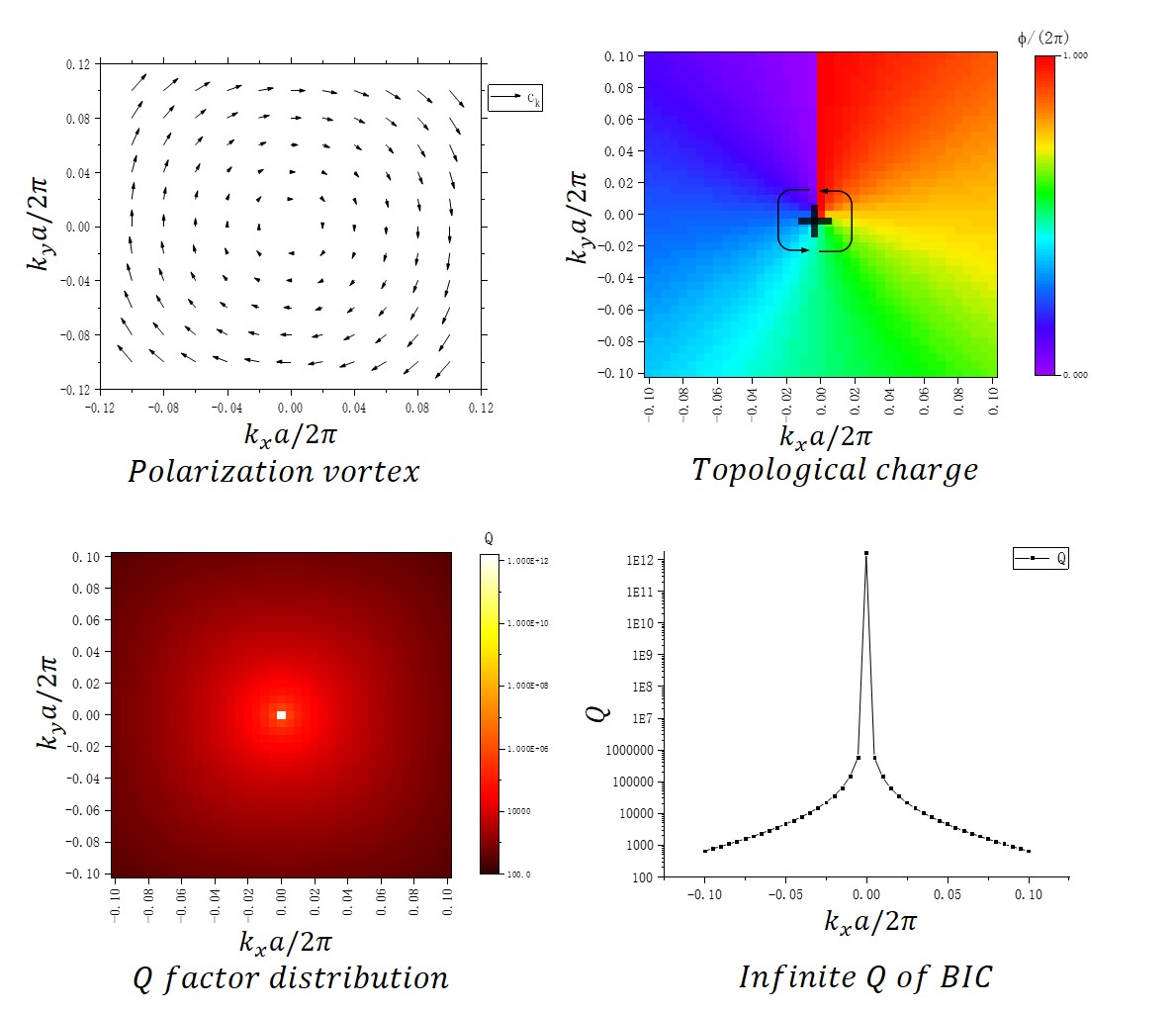
Those modes correspond to polarization vortices in the momentum space. As they have the most robust confinement ability of light compared to other eigenmodes. The polarization vortices can be characterized by their topological charges, defined as the number of roundd the polarization vector rotates when a point in momentum space goes through the vicinity of the vortex counterclockwise. As the definition suggests, topological charges are typically positive or negative integers.
The topological-protected BICs are robust under fabrication errors and defects. Ideally, they have no loss to the free space, which means they have infinite Q factors.
Our System
As a first work to explore polarization vortices outside the 1st Brillouin zone, we designed our device to have a large light cone. This design choice means the corresponding eigenmode can excite two waves in the free space: one with a -1 topological charge and one linearly polarized.
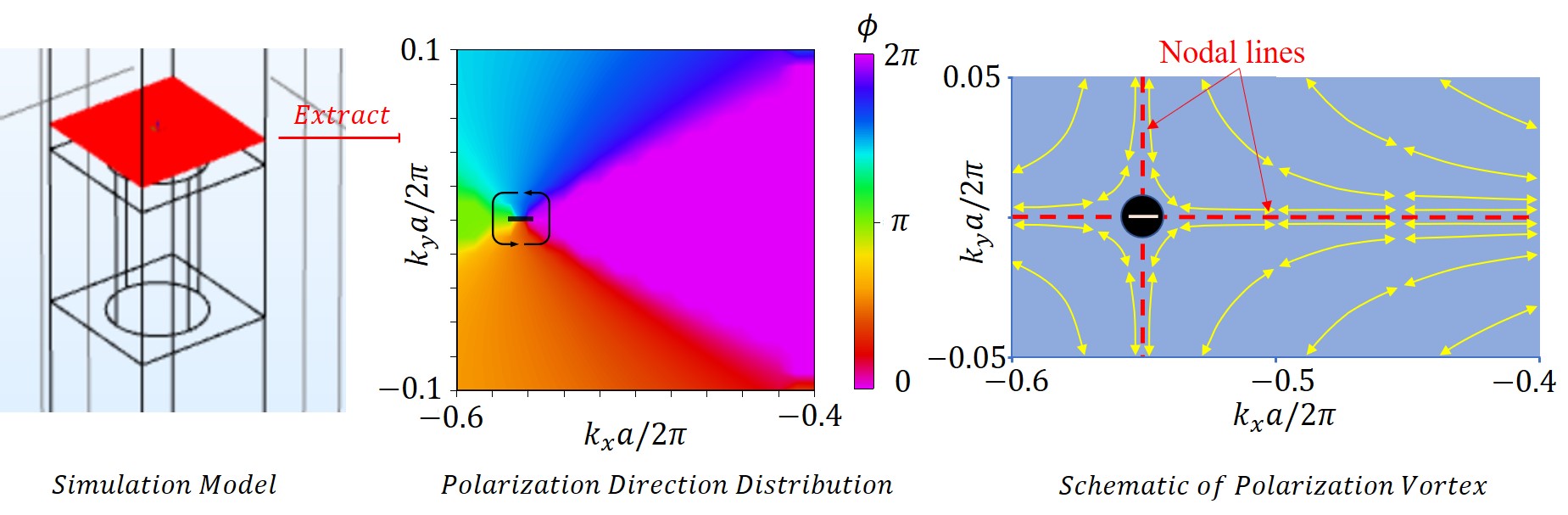
Simulation Results
The polarization vortex is found at an eigenmode with a wavelength of around 1400nm. The extracted radiation field shows the -1 topological charge in the momentum space.
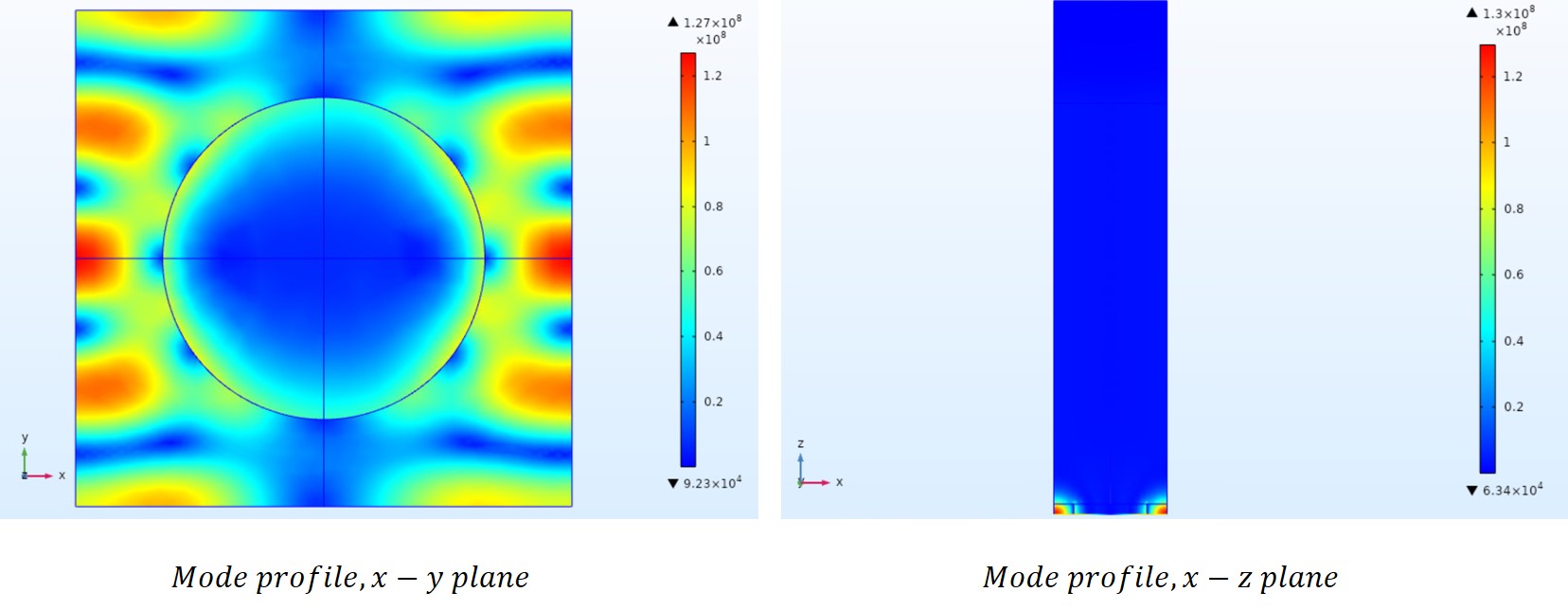
Mode profile in the real space(note that topological charges are in momentum space and constructed by eigenmodes in the vincinty of the charge). The radiation field in the free space is too weak compared to the confined electromagnetic field in photonic crystals and thus cannot be observed by eyes.
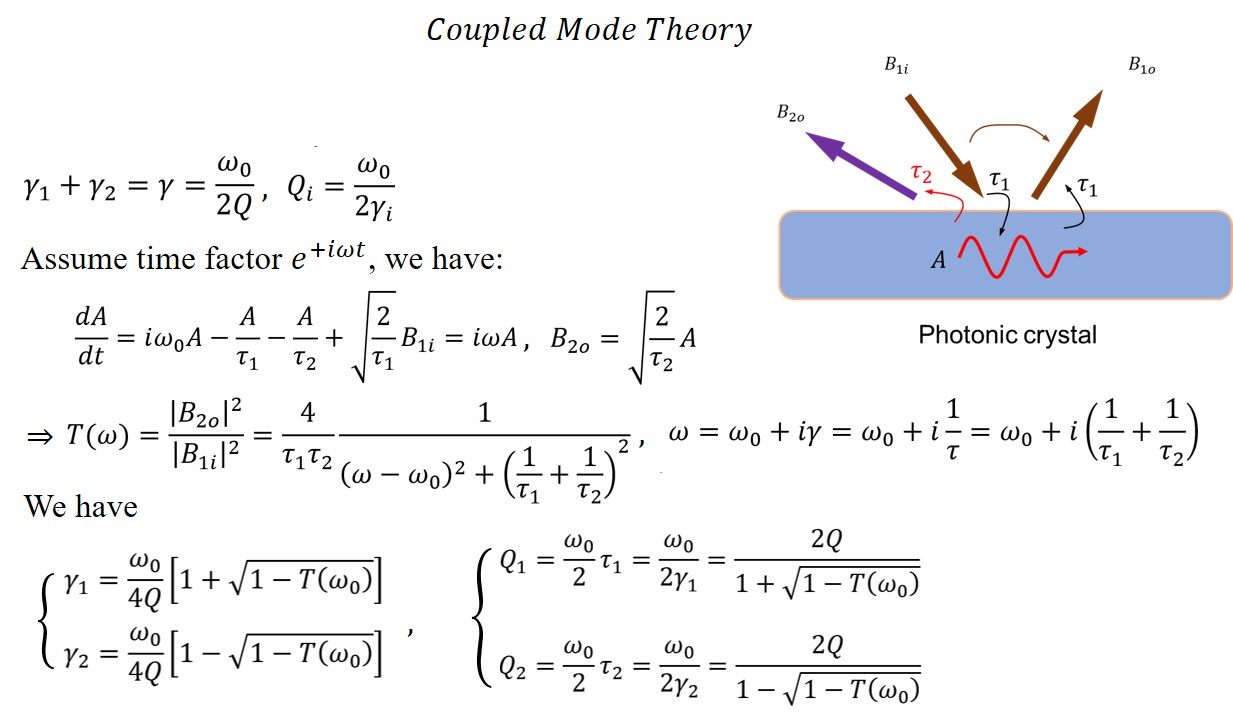
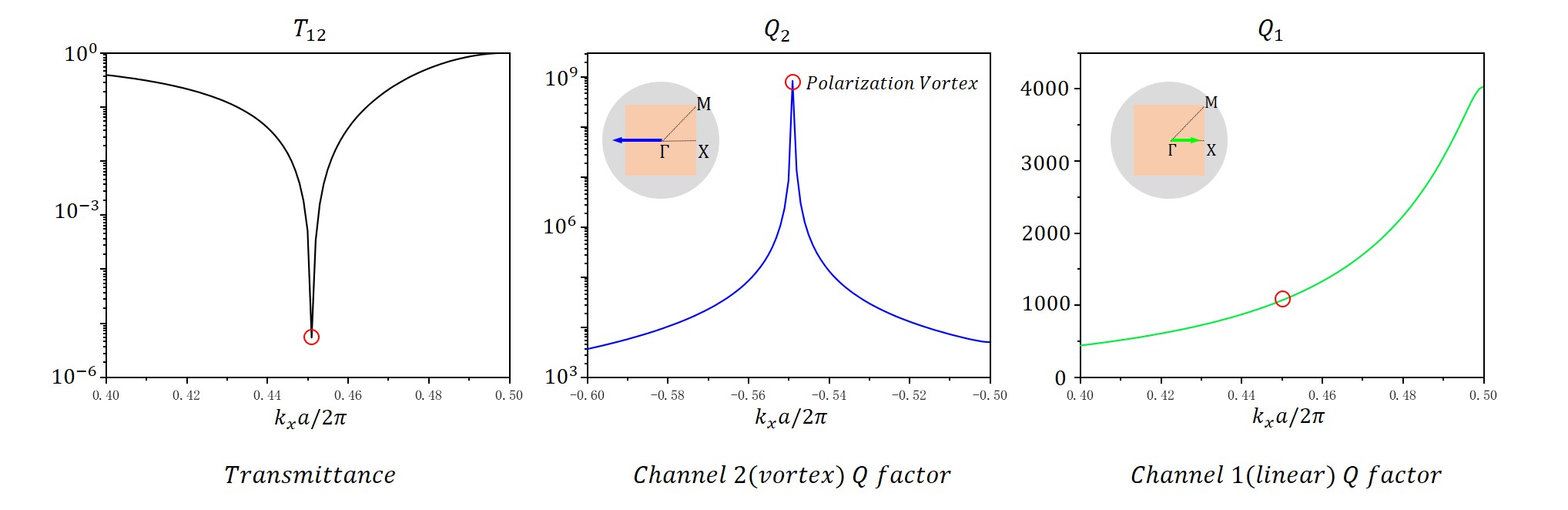
Channel Loss Analysis by Coupled Mode Theory
To verify the lossless property of the polarization vortex, we need to separate the loss into the contributions from two channels respectively. The noise introduced by the simulation method in the previous section will affect our radiation power analysis around the polarization vortex.
Therefore, instead of simulating the eigenmodes, the transmittance simulation between free space modes is performed. Based on the simulation result and analysis from coupled mode theory, we extracted the Q factor of two different channels respectively and verified the lossless property of this polarization vortex.
General Theory for Topological Vortices from First Principal
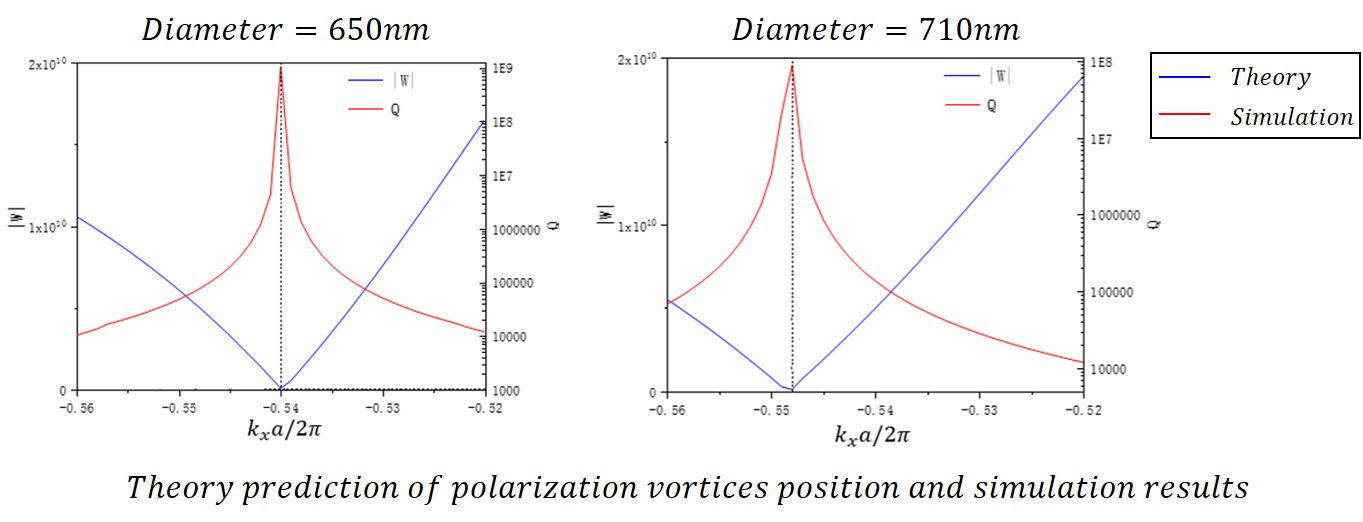
A general theory of topological vortices at any position with the existence of radiation channels is built based on some previous studies. The theory is based on basic equations which describe the wave propagation and scattering in the photonic crystals. We conclude this part with a general equation to predict the vortex position. The results from this equation agree with the simulation results in different parameters.