RISC-V Stochastic Rounding(SR) Extension

In Short

This new rounding unit supports the five existing RISC-V floating-point(FP) rounding modes and extends support for stochastic rounding. It has transprecision capability and supports different floating-point formats from FP64 to custom FP8. This new rounding unit has been integrated into OpenHW Group’s floating-point unit CVFPU (previously known as FPnew) as an extension for the RISC-V FP specification. This project was carried out at IIS, ETH.

Introduction

SR differs from other rounding modes by its unique feature: the rounding result is non-deterministic. The probability of round up(RUP) and round down(RDN) is inversely proportional to the distance to the two result candidates, i.e., the expectation value of the rounding result equals the precise value. As a result, SR does not suffer from stagnation, and some works utilize this rounding mode to do the neural network training completely in FP8.

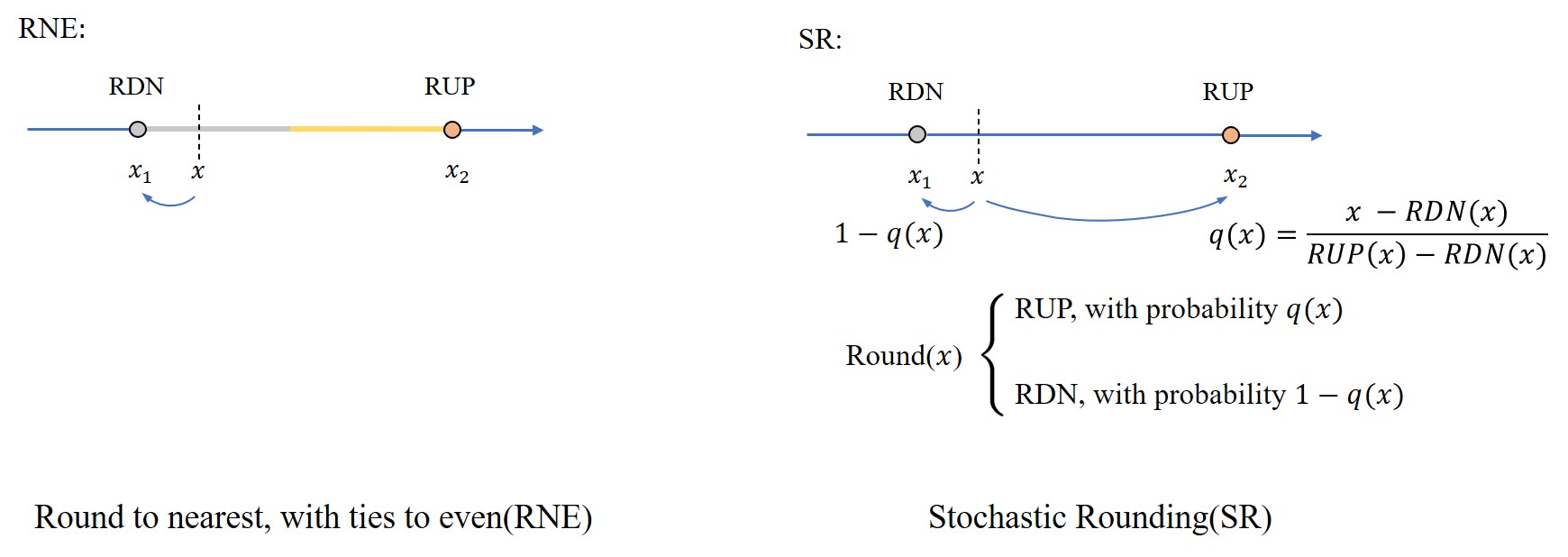
Stochastic Rounding: Algorithm

There are two ways to implement SR. The first method is to generate random numbers, add them to the precise number, and then round down. This approach is often used in software implementations where SR is realized on top of an existing rounding mode, e.g., RDN.

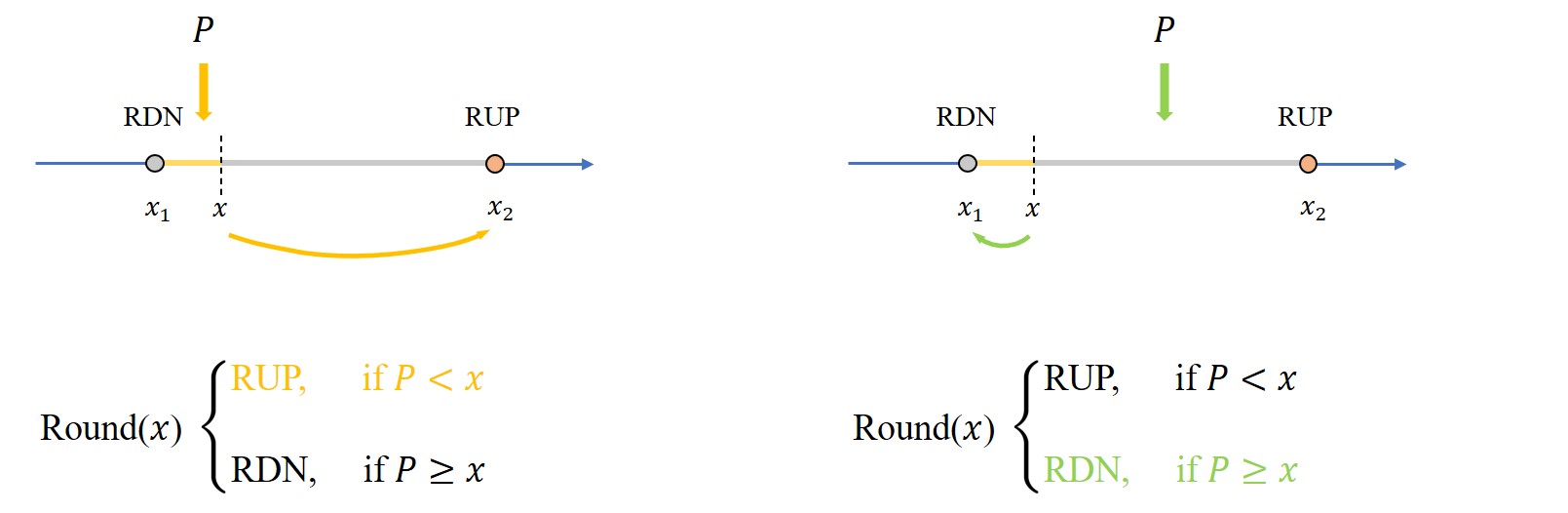
To implement SR in hardware as a stand-alone option, the second approach is used in our system: we first generate a random number between RDN and RUP results, then the output is chosen from the two candidates by the comparison result of the random number and the precise number. All operations in this approach are easy to realize in hardware using bit operations, and the corresponding datapath can be seamlessly integrated into the existing rounding unit.

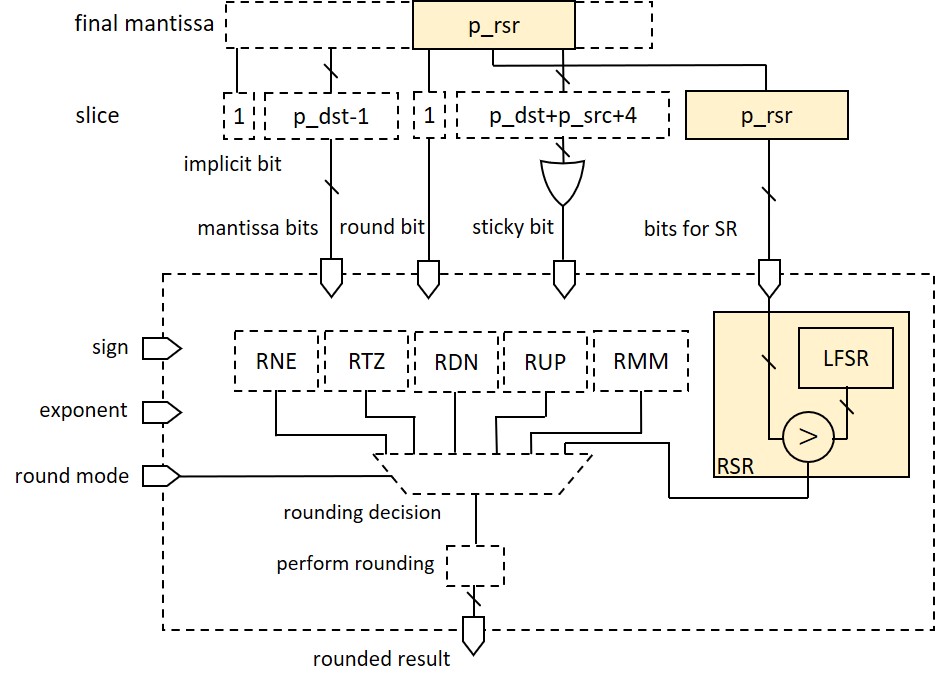
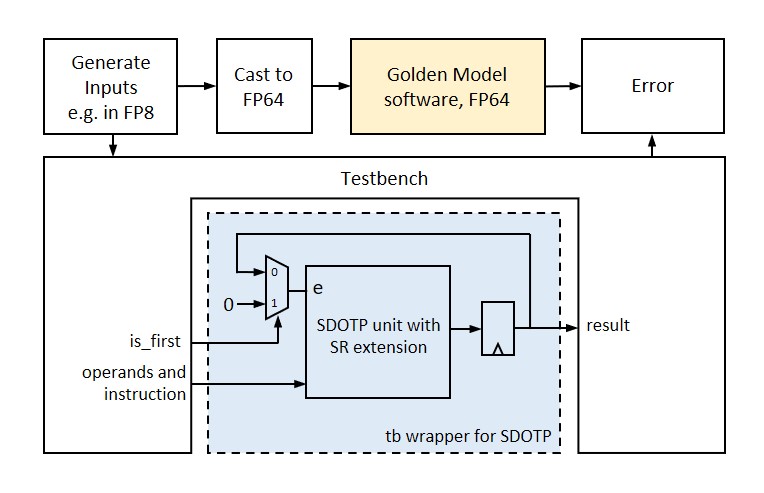
Stochastic Rounding: Testbench

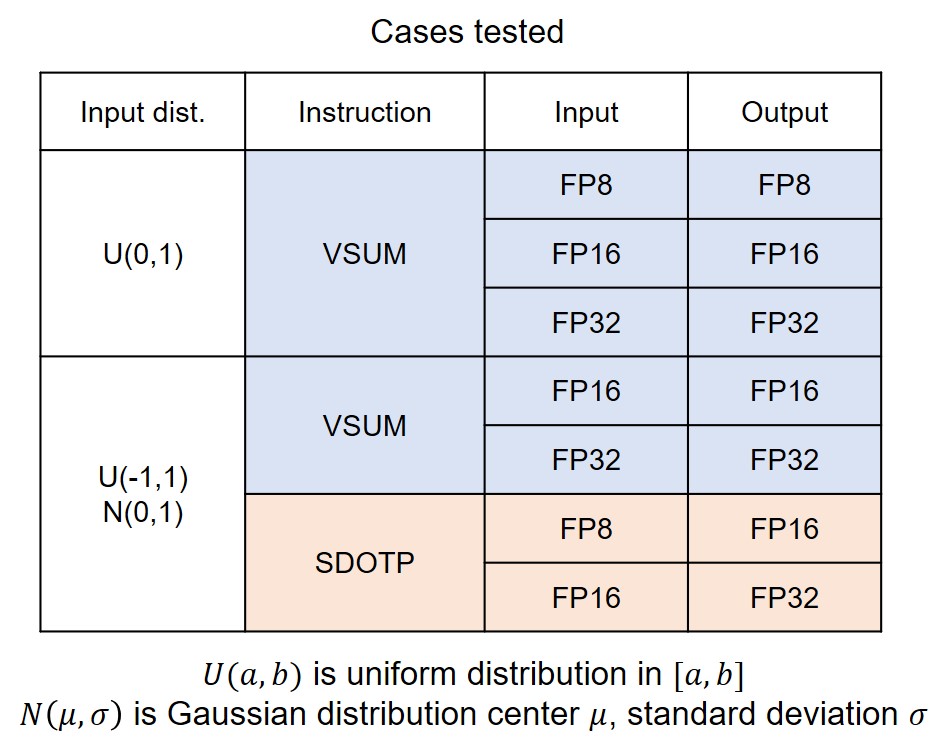
To analyze the impact of different design parameters, we analyze the accumulated error by comparing results obtained from hardware(simulation) in lower-precision and software in FP64. The comparison is done in different input distributions, FP instructions, and input/output FP formats.

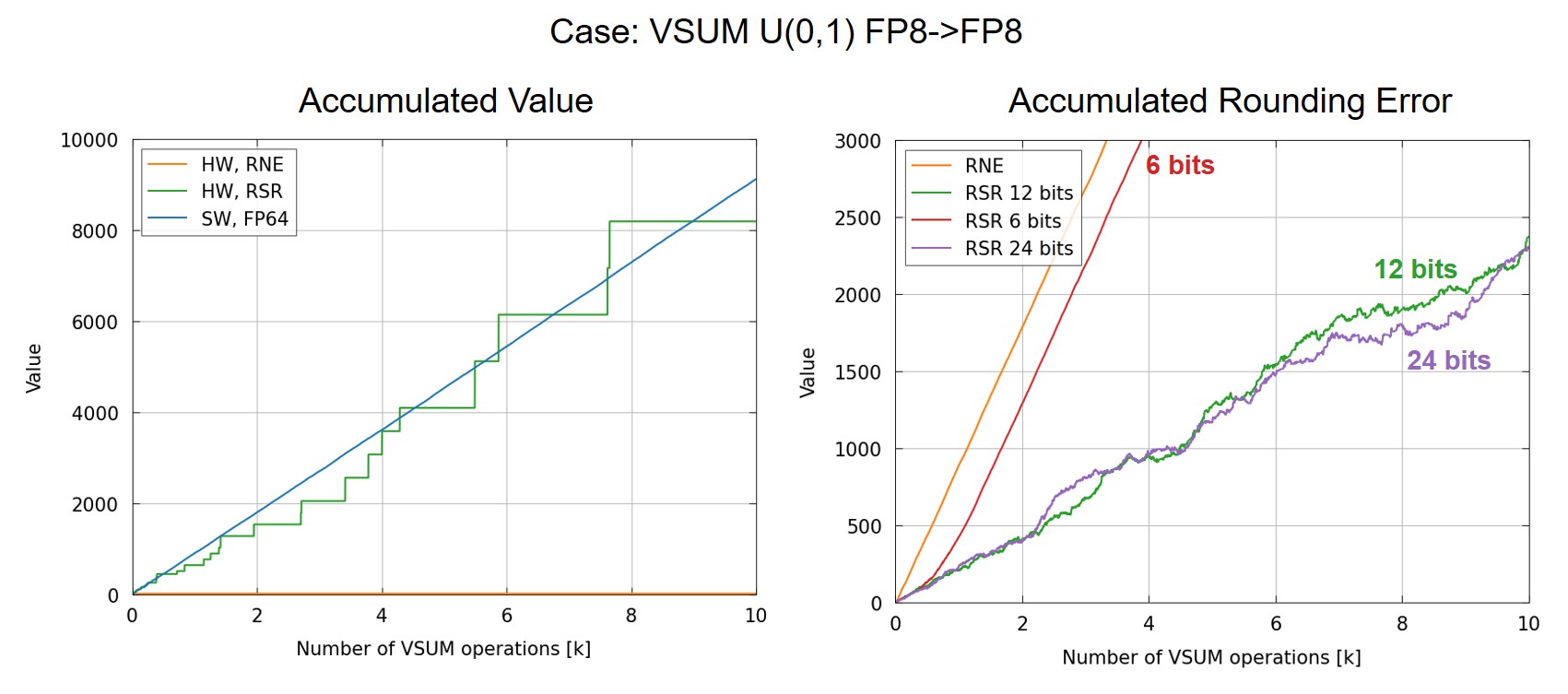
Parameter 1: Number of Bits Used for SR

The first parameter is the number of bits used for SR. Namely, this is the number of bits considered in the comparison. The number is chosen to match the integer multiple of mantissa bits in FP format. E.g. FP8 has 2-3 mantissa bits, FP16 has 11, FP32 has 24. All cases in the previous table are tested under different bit count choices: 6 bits, 12 bits, and 24 bits. We found that with >12 bits used for SR, the rounding error will not explode in 10k operations.

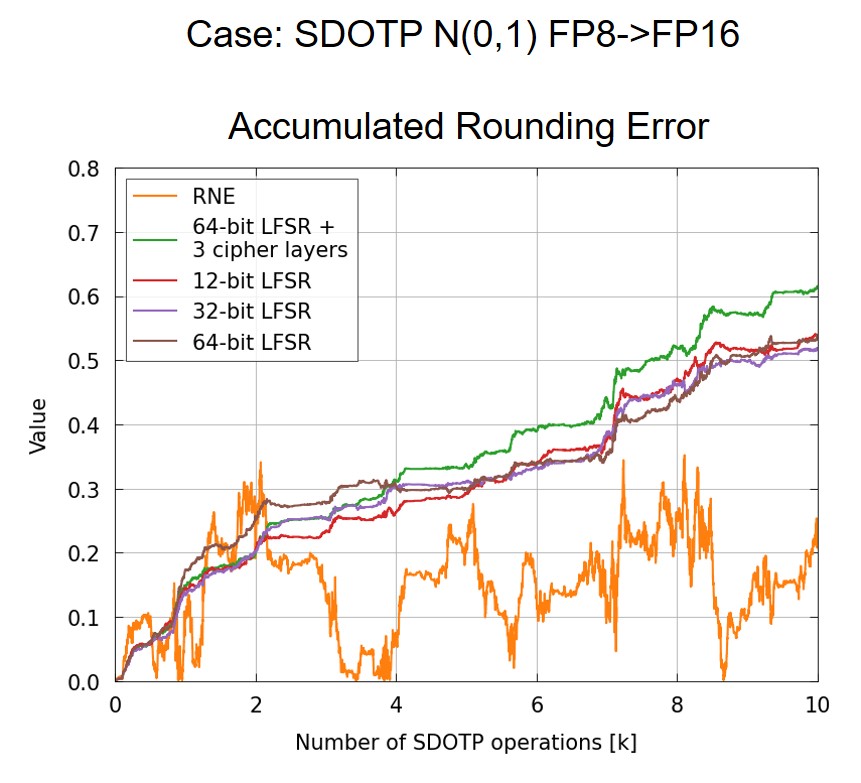
Parameter 2: Linear Feedback Shift Register(LFSR) Configurations

Another factor that may have an impact on the rounding error is the configuration of the LFSR. All cases n the previous table are tested using different LFSR configurations: different LFSR lengths, with or without cipher layers, to reshuffle the output. We found that LFSR configurations will not affect the accumulated rounding error in 10k operations.

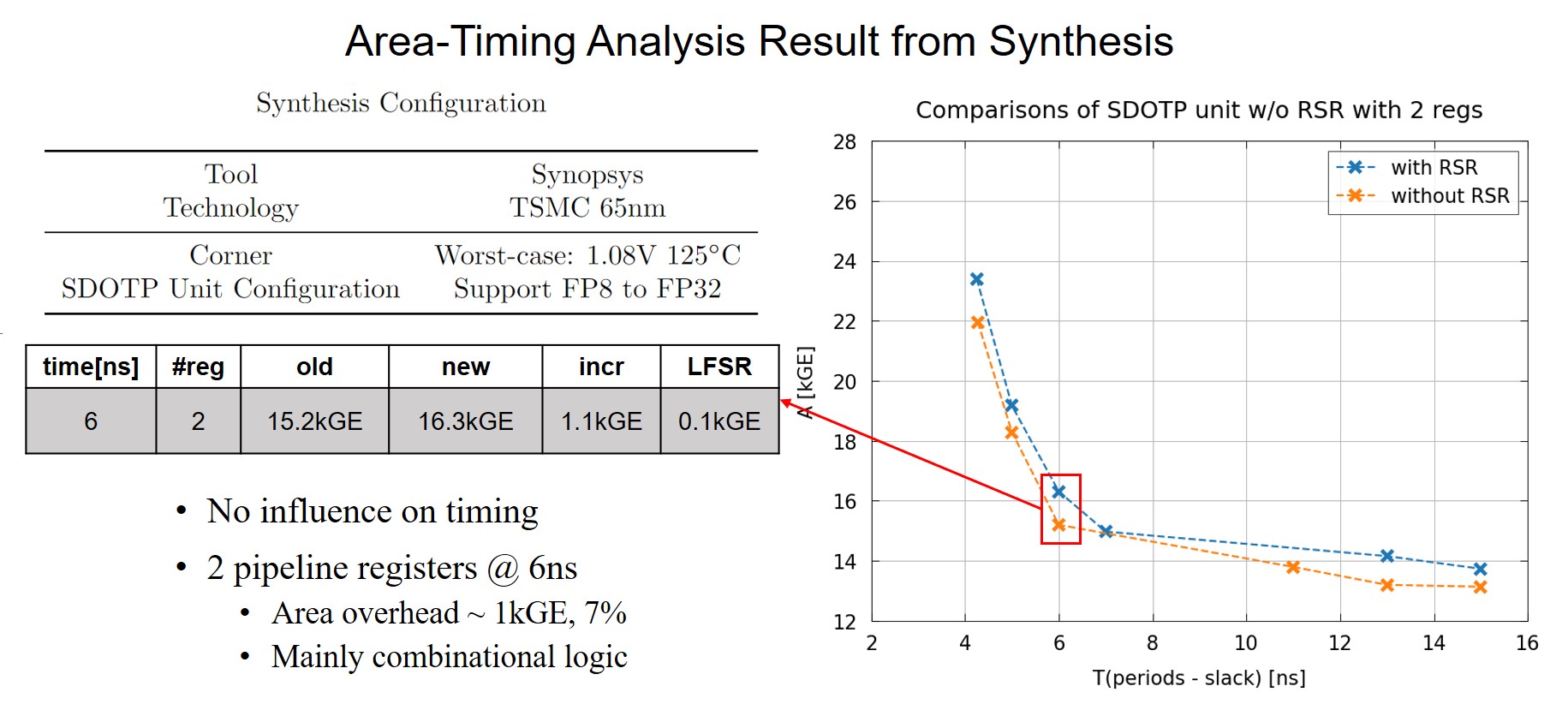
Synthesis, Area-Timing Analysis

To analyze its impact on floating-point unit’s(FPU’s) area and timing, this new rounding unit is integrated into the SDOTP unit in CVFPU(previously known as FPnew). We perform the synthesis in the TSMC 65nm technology in the worst-case corner using Synopsys. The following plot shows the area-timing analysis result. There is no influence on timing and only a 7% area increase around the optimal point.